Transformer注意力机制新发现：从work-depth模型角度看并行计算与深度复杂度优化

整理后文章：

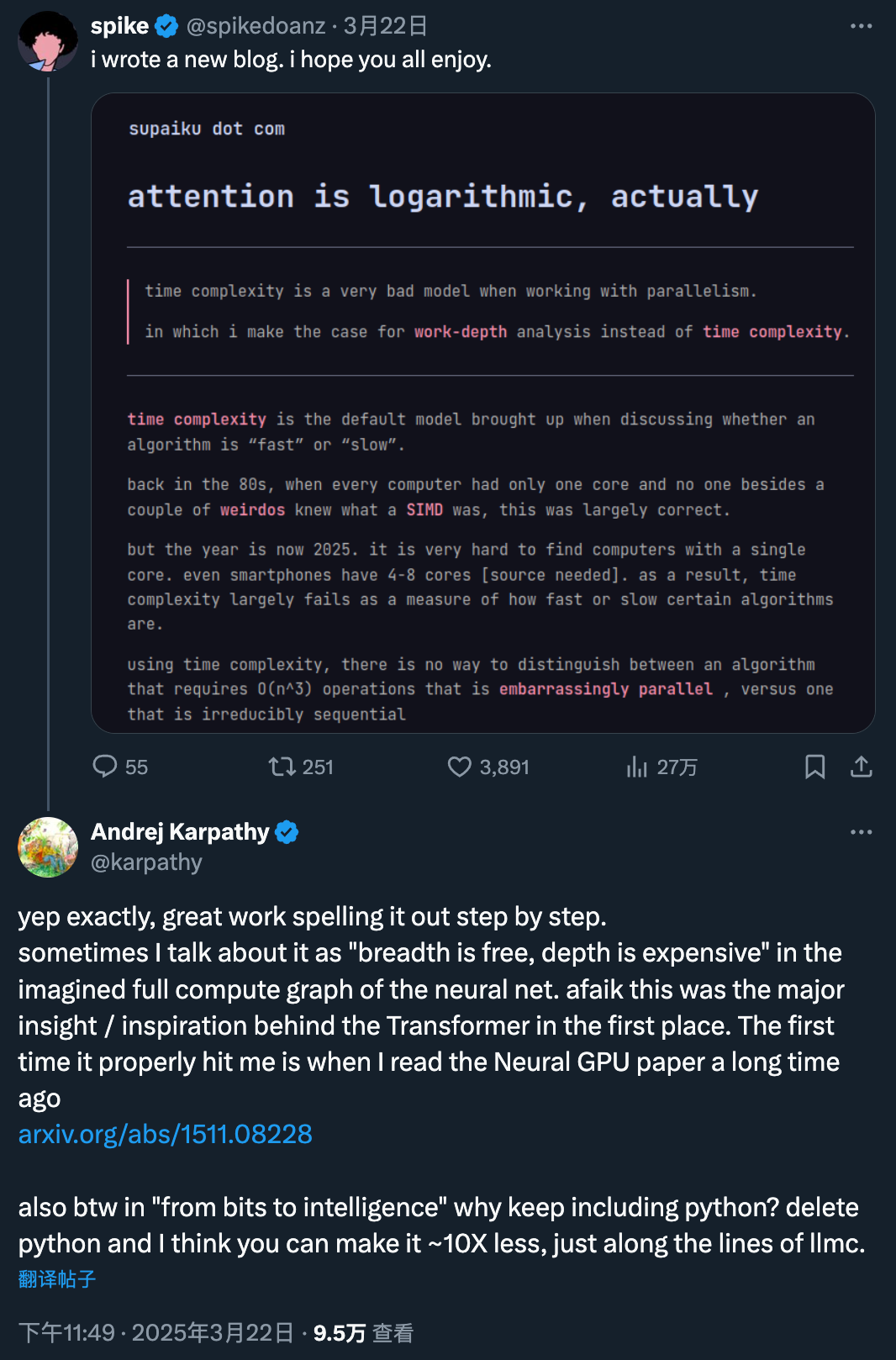
重新审视注意力机制：对数级别的复杂度？

近年来，注意力机制在人工智能领域大放异彩，尤其是在 Transformer 模型中。然而，一篇最新的博客引发了 AI 社区的热烈讨论，提出了一个全新的视角：Transformers 中实现的注意力机制，在计算复杂度上应该被视为对数级别（logarithmic）。这篇博客不仅得到了 Karpathy 的高度评价，还为理解注意力机制提供了一个全新的框架。

Karpathy 曾经这样描述神经网络的计算图：“广度是免费的，深度是昂贵的”。这一观点正是 Transformer 的核心灵感来源。作者提到，早在 Neural GPU 论文（https：//arxiv.org/abs/1511.08228）中，他就被这一思想深深震撼。此外，关于“从比特到智能”的讨论中，有人提出是否可以删除 Python 代码，以减少约 10 倍的冗余，类似于 llmc 的简化方式。

传统的注意力机制（如 Transformer 中的自注意力）计算步骤包括点积计算和 Softmax 归一化。其复杂度主要来源于矩阵乘法 QK^⊤ 和归一化操作，分别为 O(n²d) 和 O(n²)，其中 n 是序列长度，d 是特征维度。因此，研究者普遍认为标准 Transformer 的总复杂度随序列长度呈平方增长，这是其难以处理长序列的核心瓶颈。

然而，这篇博客提出了另一种分析方法——通过“work-depth 模型”来重新评估算法复杂度。这种方法不仅关注输入大小对应的操作数量，还考虑了不可并行的顺序操作的最小数量。具体来说，“work”表示原始操作的数量，而“depth”则表示不可避免的顺序操作的数量。

接下来，我们通过几个案例来深入探讨这一观点。

案例 1：逐个元素相乘
给定两个长度相同的向量 a 和 b，逐个元素相乘是将 a 中的每个元素与 b 中对应索引位置的元素相乘，并将结果存储在新向量 c 中。从时间复杂度的角度看，这似乎是线性的。但如果使用并行计算，这种操作实际上可以达到常数时间复杂度，直到达到某个临界点。

案例 2：向量求和
向量求和比逐个元素相乘更复杂，因为累加需要调用前一步的状态。不过，通过分步并行化，最终可以在 log₂(n) 步内完成所有数字的加法。

案例 3：张量积
张量积是一种基本操作，可以通过并行加载、存储和逐个相乘来实现。只要张量能够完整地装进缓存，其“depth”就是固定的。但如果张量过大，超出缓存容量，则会导致顺序处理，增加“depth”。

案例 4：矩阵乘法
矩阵乘法可以通过张量积的收缩优雅地描述。其深度复杂度为 O(1) 或 O(logn)，取决于具体实现。

案例 5：Softmax
Softmax 的深度复杂性可以通过按元素应用 e^x、收缩和按元素除法来分析。

案例 6：注意力机制
注意力机制可以通过一系列 matmuls 收缩和元素级操作的组合来实现，其渐近深度复杂度为 O(logn + logd)，其中 n 和 d 分别为序列长度和嵌入维数。

尽管如此，深度分析并非完美无缺。当内存访问模式不连续或物化变量与内存层次结构不匹配时，模型可能会失效。对于普通计算机而言，注意力的深度复杂度更像是 O(n log n)。

对未来计算的猜测
基于深度复杂度分析，未来的芯片设计可能更加注重权重的局部性和静态性。通过将权重转移到更快的内存（如 L2 缓存），可以有效降低计算复杂度，从而推动硬件性能的进一步提升。

本文来源：